深度学习中的正则化<一>

概述

深度学习的一个核心问题就是提高模型的泛化性，即不仅仅要在训练数据上表现好，还能在新输入上有更好的泛化，这些策略就是正则化。

首先来理解偏差和方差的含义：

方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力

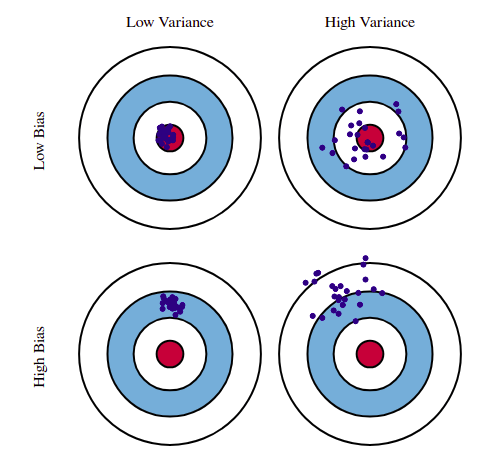
在一些过拟合的场景下，正则化会以偏差的增加来换取方差的减少。

参数范数惩罚

许多正则化方法会对目标函数J增加一个参数范数惩罚\(\Omega(\theta)\)，限制模型的学习能力，目标函数变为： \[ J'(\theta, X, y) = J(\theta, X, y) + \alpha \Omega(\theta) \] \(\alpha\)越大，对应的正则化惩罚就越大。当我们的训练算法最小化正则化后的目标函数J时，它会降低原始目标J关于训练数据的误差并同时减小在某些衡量标准下参数θ(或参数子集)的规模。

一般情况下，在神经网络中我们只对权重做惩罚而不对偏置做惩罚。精确拟合偏置所需要的数据比拟合权重少，我们不对其进行正则化也不会导致太大的方差，而且正则化偏置参数可能会导致明显的欠拟合。

L2参数正则化

\(L^2\)参数范数惩罚是最简单最常见的正则化方式，这个策略添加了一个正则项（权值向量w中各个元素的平方和），使得权重更加接近原点。这个目标函数就变成了： \[ J'(w, X, y)=\frac{\alpha}{2}w^Tw+J(w, X, y) \] 与之对应的梯度为： \[ \nabla_wJ'(w, X, y) = \alpha w+\nabla_wJ(w, X, y) \] 那么更新权重的方式也会发生变化： \[ w = w-\epsilon(\alpha w+\nabla_wJ(w, X, y)) = (1-\epsilon \alpha)w-\epsilon \nabla_wJ(w, X, y) \] 我们可以看到每步更新执行时都会先收缩权重向量。

我们进一步分析整个训练过程中会发生什么，令w为未正则化的目标函数取得最小训练误差时的权重向量，那么近似的误差函数就是： \[ J'(\theta) = J(w^*) + \frac{1}{2}(w-w^*)^TH(w-w^*) \] 其中H是J在w处计算的Hessian矩阵，当\(J'\)取得最小时，其梯度为： \[ \nabla_wJ'(w) = H(w-w^*) = 0 \] 然后我们添加上权重衰减的梯度，其中w是此时的最优点： \[ \alpha w+H(w-w^*) = 0 \]

\[ w = (H+\alpha I)^{-1}Hw^* \]

可以看到当\(\alpha\)趋向于0的时候，正则化的解w会趋向\(w^*\)。那么当\(\alpha\)增加时，在显著减小目标函数方向上的参数会保留得相对完好，而在无助于目标函数减小的方向(对应 Hessian 矩阵较小的特征值)上改变参数不会显著增加梯度，这种不重要方向对应的分量会在训练过程中因正则化而衰减掉。

简单来说，L2正则化能让学习算法对与具有较高方差的输入x更加敏感，使得与输出目标的协方差较小的特征的权重收缩，

L1参数正则化

L1正则化则是添加一个另外的正则化项（权值向量w中各个元素的绝对值之和）： \[ J'(w, X, y)=\alpha||w||_1+J(w, X, y) \] 对应的梯度为： \[ \nabla_wJ'(w, X, y) = \alpha sign(w)+\nabla_wJ(w, X, y) \] 其中sign(w)只是简单地取w各个元素的正负号，其中若w>0，则sign(w)=1；若w<0，则sign(w)=−1；若w=0，则sign(w)=0。

相比L2正则化，L1正则化会产生更加稀疏的解，这里的稀疏指的是最优值中的一些参数为0。由L1正则化导出的稀疏性质被广泛用于特征选择机制，从可用的特征子集中选择出有意义的特征。