反向传播和其他的微分算法
概述
在训练过程中,前向传播可以向前直到它产生一个标量代价函数\(J(\theta)\),而反向传播会计算代价函数关于参数的梯度,即\(\nabla_\theta J(\theta)\)。
计算图
我们将计算形式转化为图形,形成计算图。那么我们每一个结点代表一个变量,操作则是一个或者多个变量的简单函数,我们定义一个操作仅仅返回单个输出变量。
如果变量 y 是变量 x 通过一个操作计算得到的,那么我们画一条从 x 到 y 的有向边。

微积分中的链式法则
微积分中的链式法则用于计算符合函数的导数。
假设x是实数,f和g是从实数映射到实数的函数。假设y=g(x)并且z=f(g(x))=f(y)。那么就有: \[ \frac{dz}{dx} = \frac{dz}{dy} \frac{dy}{dx} \] 如果向向量的情况扩展: \[ \frac{\alpha z}{\alpha x_i} = \sum_j \frac{\alpha z}{\alpha y_i} \frac{\alpha y_i}{\alpha x} \\ \nabla_x{^z} = (\frac {\alpha y} {\alpha x})^T \nabla_y{^z} \] 这个$ {x}$是g的Jacobian矩阵。
当然,也可以将反向传播应用到任意维度的张量,在我们运行反向传播之前,将每个张量变平为一个向量,计算一个向量值梯度,然后将该梯度重新构造成一个张量。
递归地使用链式法则来实现反向传播
使用链式法则,我们可以直接写出某个标量关于计算图中任何产生该标量的梯度的代数表达式,但一般计算机在计算时会引入一些额外的考虑。 \[ \frac{\alpha u^{(n)} }{\alpha x^{(j)} } = \sum_{i:j \in Pa(u^{(i)})} \frac{\alpha u^{(n)} }{\alpha u^{(i)} } \frac{\alpha u^{(i)} }{\alpha u^{(j)} } \] 考虑这种计算图,在计算梯度时导致子表达式重复计算:
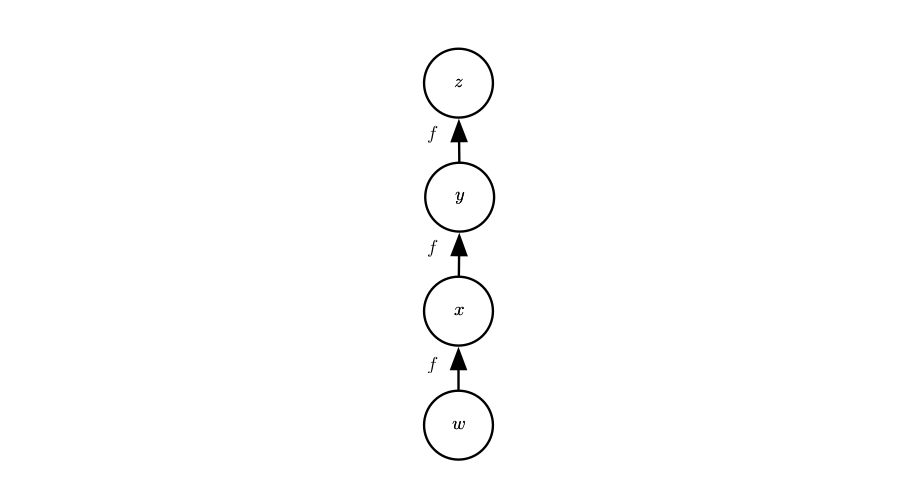
为了计算z对w的梯度: \[ \frac{\alpha z}{\alpha w} \\ =\frac{\alpha z}{\alpha y} \frac{\alpha y}{\alpha x} \frac{\alpha x}{\alpha w} \\ =f'(y)f'(x)f'(w) .............1\\ =f'(f(fw)) f'(f(w)) f'(w) .............2 \] 对于1式,我们采用的实现方式是仅仅计算f(w)一次,并存储起来,这种方式减少了运行时间;
而对于2式,每次只在需要时重新计算f(w),在存储受限时它是有用的。
符号到符号的导数
代数表达式和计算图都对符号或不具有特定值的变量进行操作,这些代数或者基于图的表达式就是符号表示。一些反向传播的方法采用计算图和一组用于图的输入的数值,然后返回在这些输入值处梯度的一组数值。我们将这种方法称为 符号到数值的微分。这是Torch和Caffe使用的方法;
另一种方法则是采用计算图以及添加额外的结点到计算图中,其提供了我们需要导数的符号描述,这是Theano和TensorFlow采用的方法。
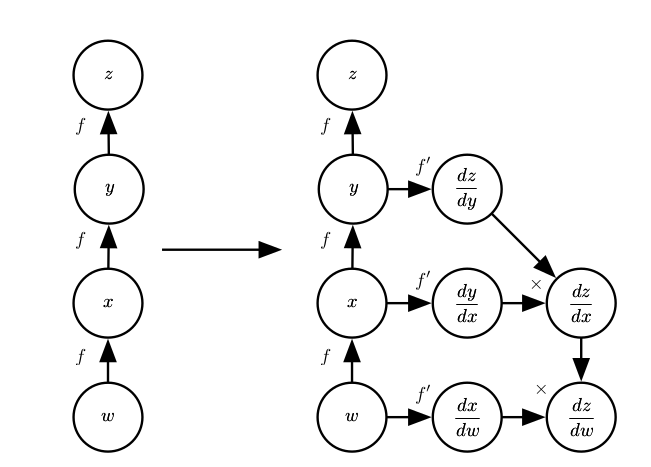
一般化的反向传播
反向传播算法比较容易理解,其实就是为了计算某个标量z关于图中它的一个祖先x的梯度,我们首先观察到它关于z的梯度由1给出,然后,我们对图中z的每个父节点的梯度进行计算,通过现有的梯度乘以产生z的操作的Jacobian。如果从z触发经过多条路径到达父结点,我们应该对不同路径上的梯度进行求和。
求解这种表达式\(\frac{\alpha u^{(i)} }{\alpha u^{(j)} }\)的时候,相同的计算可能会重复多次,为了避免重复计算,我们利用存储的中间结果\(\frac{\alpha u^{(n)} }{\alpha u^{(i)} }\)来进行补充计算。