Backpropagation and Neural Networks

计算图：每个节点表示一个计算步骤

反向传播：链式法则的递归调用

用微积分可能无法求解

可以组合某些结点成更复杂的结点，只要能求解导数即可

add gate, max gate

如果有一个结点连接到了多个结点

雅克比矩阵

方向转播：利用链式法则递归计算表达式的梯度的方法

简单理解

其实学过微积分的同学应该都能理解导数的含义，简单概括就是变量变化导致的函数在该变量方向上的变化率，指明了整个表达式对于该变量的敏感度。 \[ f(x, y) = x + y -> \frac{df}{dx} = \frac{df}{dy} = 1 \] 同样对于取最大值的操作： \[ f(x, y) = max(x, y) -> \frac{df}{dx} = 1(x>=y) \frac{df}{dy} = 1(y>=x) \]

使用链式法则计算符合表达式

考虑这样的一个符合函数\(f(x, y, z)=(x+y)z\)，将其分为两个部分\(q=x+y和f=qz\)。根据链式法则，将梯度表达式连起来的方式就是相乘： \[ \frac{\alpha f}{\alpha x} = \frac{\alpha f}{\alpha q} \frac{\alpha q}{\alpha x} \]

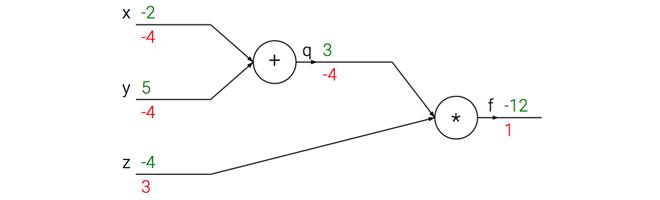
这个计算线路图展示了计算的视觉化过程，前向传播从输入计算到输出（绿色），后向传播从尾部开始。

反向传播的理解

在前向传播过程中计算两个东西：输出和局部梯度。这样在反向传播的时候，就可以将上游回传的梯度乘以局部梯度。

至于常见的几种单元，诸如加法门单元、取最大值门单元、乘法门单元都比较好理解。例如在线性分类器中，权重和输入进行点积\(w^T x_i\)，假设所有的输入样本都乘以1000，那么权重的梯度将会增大1000倍，这样就必须降低学习率来弥补。

小结

反向传播，简单的理解就是复合函数的链式法则。

参考资料

http://www.cnblogs.com/charlotte77/p/5629865.html