损失函数与优化

##损失函数

线性分类器：高维空间下的线性决策边界。

loss function：判断我们分类器的效果，损失函数有多种版本：softmax和svm

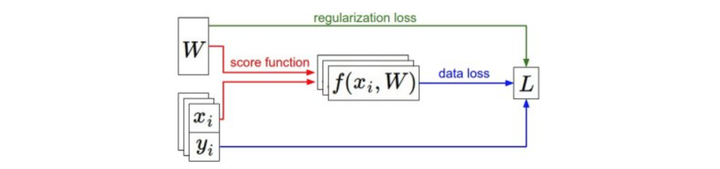
svm的实现公式如下： \[ L = \frac1N\sum_{i}\sum_{j\neq y_i} [max (0, f(x_i, W)_j - f(x_i, W)_{y_i} + 1)] + \alpha R(W) \] 通过上面的公式可看到，如果基于参数集W做出的分类预测与真实情况比较接近，那么计算出来的L就会比较小。因此，我们需要做Optimization，寻找使得顺势函数最小化的参数W的过程。

multiclass svm

如果真实分类的分数比其他类分数高很多（一般我们可以加上一个边界），我们是满意的；否则，我们认为会得到一些loss。

svn损失函数最小值为0，最大值是无穷大，看hinge图。

如果所有的score都接近0，并且相差不大，那么损失函数为C-1。

使得loss为0的W不是唯一的，可以加倍，那么边界也会加倍。

不需要关心分类器在训练集上的表现，避免过拟合。因此，我们可以对loss进行正则化，增加一个正则项。

L2正则化、L1正则化

softmax classifier

使得概率接近1

刚开始应该是-logC

最优化

SVM损失函数是一个凸函数，但我们最终的目标并不仅仅是对凸函数进行优化，而是能够最优化一个神经网络。

我们使用的策略是follow the slope。即根据梯度在权重空间W中寻找一个方向，沿着该方向能够降低损失函数的损失值。

计算梯度有两种方法：

有限差分法

为了计算梯度，我们是在梯度负方向进行更新，这样才能使得损失函数值降低；另外，我们要注意步长的影响，梯度指明了函数在哪个方向是变化率最大的，但步长则指明了在这个方向上走多远。步长也叫学习率。小步长下降稳定，但进度慢，大步长则是进展快，但风险高，容易错过最优点。

从效率来看，有限差分法每走一步就需要计算n次损失函数的梯度（n为参数数量），这是一种效率极低的策略

微积分计算梯度

用SVM的损失函数在某个数据点上的计算为例： \[ L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + \Delta) \right] \] 然后对函数进行微分。比如对\(w_{y_i}\)进行微分： \[ \nabla_{w_{y_i}} L_i = - \left( \sum_{j\neq y_i} \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) \right) x_i \] 其中1是一个示性函数，如果括号中的条件为真，那么函数值为1，如果为假，则函数值为0。这是对正确分类的梯度，至于不正确的分类的梯度计算： \[ \nabla_{w_j} L_i = \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) x_i \] 以下就是，在梯度下降过程中，我们计算权重的梯度，然后使用它们来实现参数的更新